ParticleBox

Overview

ParticleBox is a high-performance C++ physics simulator capable of rendering thousands of interacting particles in real-time. It leverages modern C++17 features, SIMD acceleration (Apple Accelerate), and multithreading (OpenMP/GCD) to maximize throughput on multi-core systems.

Key Optimization Techniques

• Spatial Partitioning: Grid-based subdivision reduces collision complexity from \(O(n^2)\) to near \(O(n)\) using efficient bitwise indexing.
• Parallel Processing: Dynamic workload distribution via OpenMP and Grand Central Dispatch (GCD) ensures optimal core utilization.
• SIMD Acceleration: Vectorized math operations using Apple's Accelerate framework and compiler auto-vectorization for massive throughput.
• Memory Optimization: Contiguous memory layouts and pre-allocation strategies minimize cache misses and runtime overhead.

Gallery

Background & Physics

Collision Detection

To maintain performance, we calculate squared distances to avoid expensive square root operations in the inner loop:

\[ d^2 = (p2.x - p1.x)^2 + (p2.y - p1.y)^2 \]

A collision occurs when \(d^2 < (r1 + r2)^2\). For force calculations requiring normalized vectors, we employ the Fast Inverse Square Root algorithm.

Force Calculation

Repulsion forces are applied proportional to the overlap depth \(\delta\):

\[ \mathbf{F}_r = -\hat{\mathbf{n}} \cdot \text{repulsionStrength} \cdot \delta \]

Integration

State updates are handled via Semi-Implicit Euler integration for stability and speed:

\[ \mathbf{v}_{t+\Delta t} = \mathbf{v}_t + (\mathbf{F}_t / m) \cdot \Delta t \] \[ \mathbf{p}_{t+\Delta t} = \mathbf{p}_t + \mathbf{v}_{t+\Delta t} \cdot \Delta t \]

Implementation Details

System Architecture

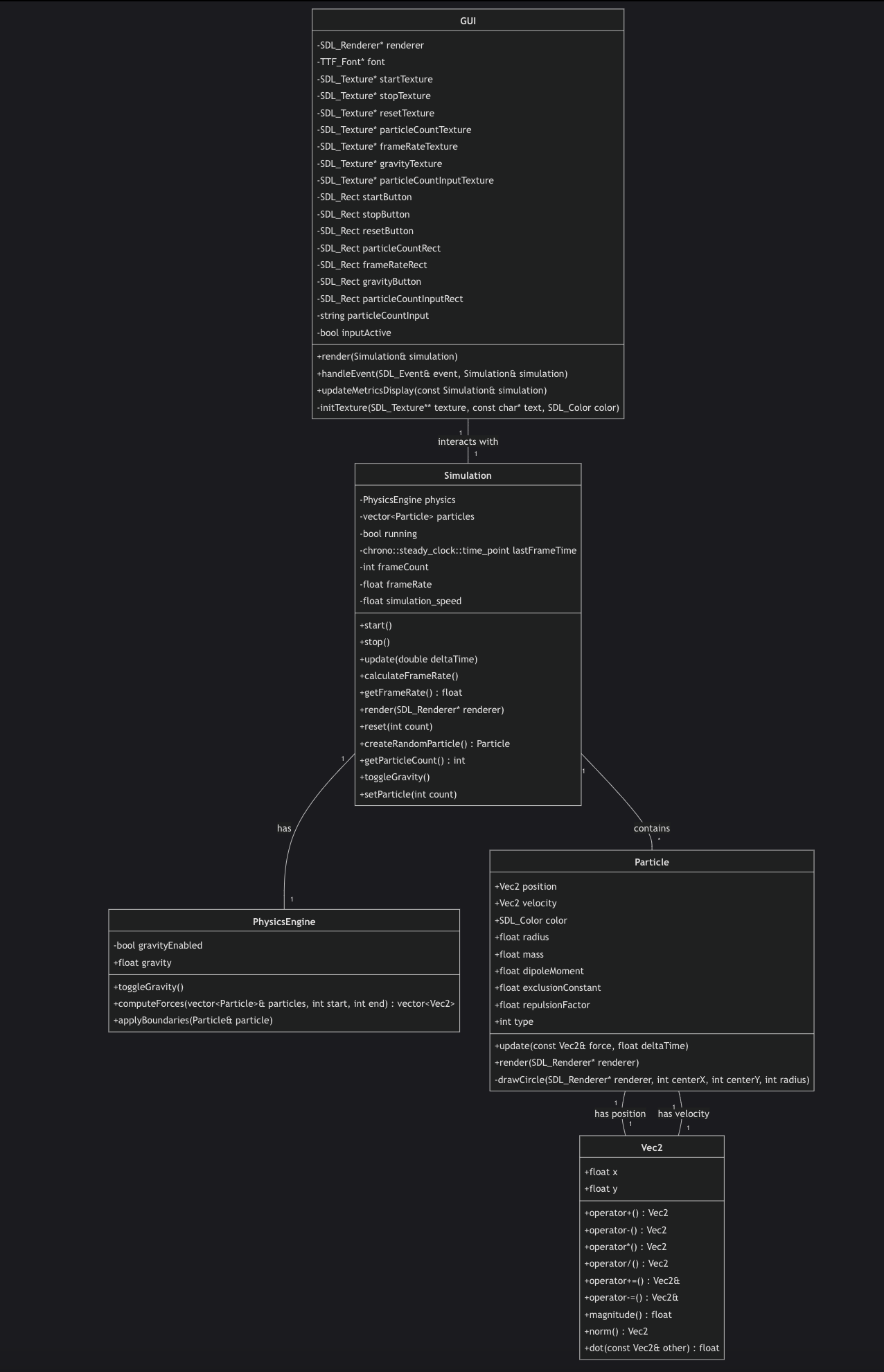
The codebase is structured for modularity and performance:

• Simulation Core: Manages particle lifecycle, state, and the main update loop.
• Physics Engine: Handles force accumulation, collision resolution, and boundary constraints.
• Rendering: Decoupled rendering pipeline using SDL2 for efficient visualization.

Spatial Partitioning

The grid system uses a flat-array structure to optimize neighbor lookups. Particles are mapped to cells using bitwise spatial hashing, allowing for constant-time access to potential collision candidates.

Multithreading Strategy

The engine implements a platform-agnostic threading model:

• Apple Silicon: Native GCD implementation for low-overhead task scheduling.
• Cross-Platform: OpenMP and std::async fallbacks for Windows/Linux environments.

SIMD & Memory

Vector operations are accelerated using simd_float2 on macOS, while std::vector pre-allocation prevents runtime resizing. Data is stored in an Array of Structs (AoS) pattern, optimized for the specific access patterns of the simulation loop.

Performance Analysis

Profiling with Instruments and VTune guided the optimization process, resulting in:

• Algorithmic Efficiency: Spatial partitioning eliminated the primary \(O(n^2)\) bottleneck.
• Compute Density: SIMD vectorization significantly increased floating-point throughput.
• Scalability: The multithreaded architecture scales linearly with available cores, maintaining high frame rates even under heavy load.

Technology Stack

• Core Language: C++17
• Graphics/Windowing API: SDL2, SDL2_ttf
• Build System: Make (Makefile) with platform detection and optimization flags (-O3, -march=native, -mcpu=apple-m1, -ftree-vectorize, -fopenmp).
• Parallelism: OpenMP, C++11 Threads (std::async, std::future), Apple Grand Central Dispatch (GCD)
• SIMD: Apple Accelerate Framework (simd/simd.h), Compiler Auto-Vectorization (via flags)
• Key Optimization Techniques: Spatial Partitioning (Grid), Multithreading, SIMD, Memory Pre-allocation, Fast Math Algorithms, Texture Caching.
• Profiling Tools: Valgrind, Intel VTune, Apple Instruments
• Development Environment: Visual Studio Code, CLion (User specified)
• Platform Support: Windows, macOS (with Apple Silicon optimizations), Linux.